格式:pdf
大小:516KB
頁數: 15頁
實用標準文案 精彩文檔 圓錐曲線中的最值取值范圍問題 90.已知 1 2,F F 分別是雙曲線 22 2 2 x y a b =l( a>0,b>0)的左、右焦點, P為雙曲線上的一點, 若 0 1 2 90F PF , 且 21PFF 的三邊長成等差數列. 又一橢圓的中心在原點, 短軸的 一個端點到其右焦點的距離為 3 ,雙曲線與該橢圓離心率之積為 5 6 3 。 ( I )求橢圓的方程; (Ⅱ)設直線 l 與橢圓交于 A,B兩點,坐標原點 O到直線 l 的距離為 3 2 ,求△ AOB面 積的最大值. 90.解:設 nPFmPF ||,|| 21 ,不妨 P在第一象限,則由已知得 ,065 .22 ,)2( ,2 22222 caca mcn cnm anm ,0562 ee 解得 15 ee 或 (舍去)。設橢圓離心率為 . 3 65 5, ee 則 . 3 6 e 可設橢圓的方程為


格式:pdf
大小:78KB
頁數: 11頁
沈陽理工大學裝備工程學院綜合課程設計 C3 1 1 緒 論 雷電是一種大氣自然現象,對人類社會而言,雷電有時也會造成自然災害。人與自 然總體上是和諧發展的, 這是社會進步的前提, 雷電災害的范圍和表現形式在這發展過 程中也在發生變化,于此同時,雷電防護科學技術也在人類認識自然,抵御自然災害過 程中不斷發展。 從久遠的過去開始, 雷電就對人類、 人類賴以生存的自然資源和人類創造的物質文 明構成巨大的威脅, 例如,森林火災有 50%以上因雷電引發; 人們居住生活的建筑物屢 遭雷電破壞;電力、石化等工業設施常因雷擊而發生災難性事故。不難看出,雷電災害 的范圍隨社會經濟發展而擴大,其表現形式隨其范圍擴大而復雜。 因此,提高雷電防護科技水平勢在必行。 富蘭克林發明避雷針之后,這一防雷工程技術延續了百余年毫無發展,不僅是由于 人類對雷電的認識停滯不前, 而且還由于實際需要沒有變化, 避雷針還未顯出其
熱門知識
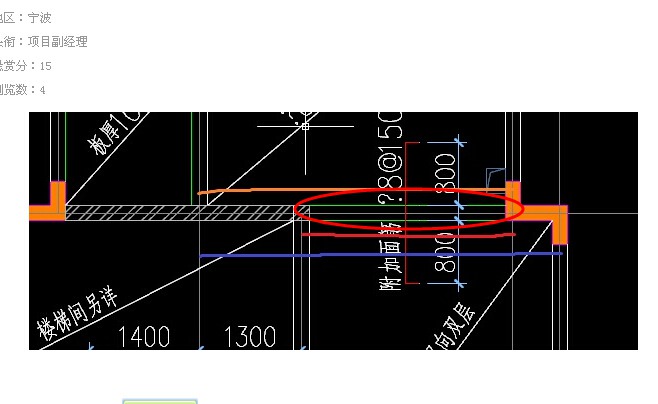
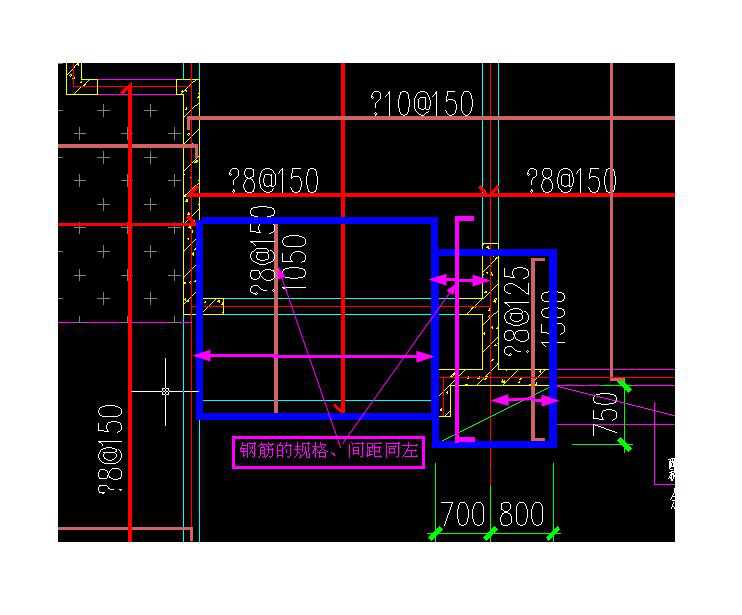
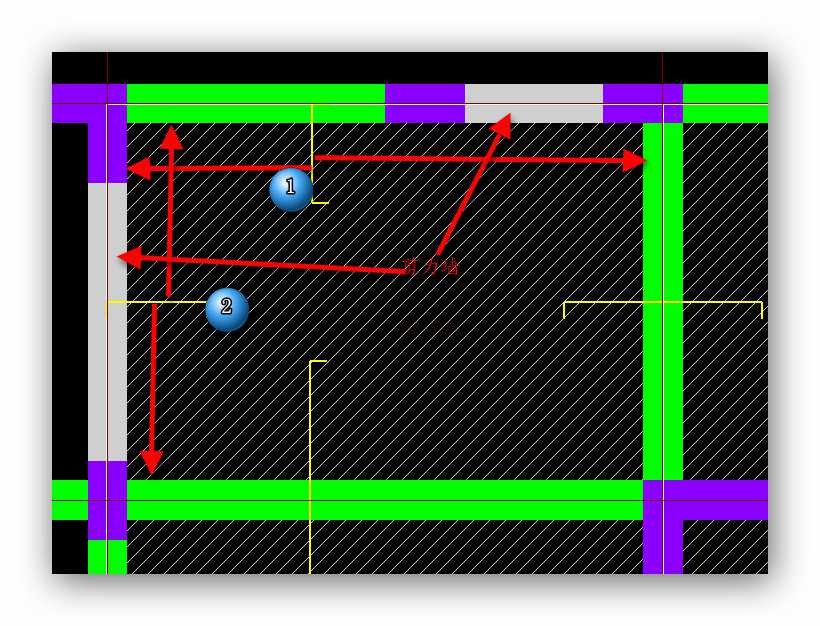
負筋線范圍問題-
話題: 工程造價renhui510510
-
話題: 工程造價jc_chenghao
-
話題: 造價軟件cc19861017
-
話題: 造價軟件huiwong920
精華知識
負筋線范圍問題最新知識
負筋線范圍問題相關問答
負筋線范圍問題-
話題: 工程造價qiutian001
- 看圖看鋼筋圖
- 看這道梁配筋對
- 抗拔樁分段配筋
- 抗水板中鋼筋的計算
- 抗震鋼筋當做普通鋼筋送檢
- 抗震鋼筋有標準
- 抗震鋼筋問題
- 空心屋面板鋼筋大小及根數
- 空心板鋼筋和砼的處理
- 孔樁鋼筋結算
- 應用亞溫淬火工藝解決45鋼槽型螺母淬裂問題的探索
- 有關建筑工程造價管理面臨的問題與其處理手段
- 定征復合板材粘接層性質的非線性超聲蘭姆波方法
- 以BIM為基礎的裝配式建筑全生命周期管理問題
- 在建筑行業建立農民工工資保證金制度若干問題的思考
- 圓形隧道反向曲線隧道中心線兩種偏移計算方法的比較
- 中國水環境污染治理社會化資金投入現狀、問題與對策
- 醫用潔凈空調系統設計調試中易忽視的問題及設計優化
- 園林景觀工程在推進城鄉宜居環境建設中的問題及思考
- 在砌塊配筋砌體中使用的新型鋼筋直螺紋連接套筒
- 中國現代化鋼筋加工工藝與傳統鋼筋加工工藝相比優勢
- 圓形截面預應力鋼筋混凝土懸臂式支護樁的分析與應用
- 張家口市中心城區污水排水管網在線監測系統設計
- 應用貴州省雨洪公式計算施工期設計洪水需注意的問題
- 中國2010年上海世博會園區管線綜合管溝管理辦法
- 中國鋁業山東分公司新建20萬噸4A沸石生產線開工
- 醫院弱電系統線纜敷設及柜箱安裝施工方案與技術措施
- 負筋在廣聯達里面的布置
- 負控箱和計量箱的區別
- 負控裝置怎么套定額
- 負離子發生器的價格
- 負離子空氣凈化器風扇不轉
- 負彎矩筋是什么樣
- 負彎矩與負彎矩筋問題
- 負溫轉正溫的試塊怎么留置
- 負五度sbs防水卷材什么意思
- 負壓風管與正壓風管的區分
- 負壓風機18000m3h價格
- 負壓風機和排氣扇區別
- 負壓風機價格多少
- 負壓風機價格一般是多少
- 負壓風機就是排風扇
- 負壓管道中的水如何排出
- 負壓開關壞會有什么影響
- 負一層是否計算垂直封閉費
- 負一層算主體還是基礎
- 負載端空氣開關跳閘原因
- 負載均衡工程師薪水
- 負載是電阻
- 負載轉矩怎么計算
- 附的結構是什么
- 附加板底部鋼筋
- 附加吊筋是怎么計算的
- 附加防水層的計算
- 附加鋼筋的定義
- 附加箍筋6d@50是什么意思
- 附加箍筋的計算