（一）輪齒的受力分析

進行齒輪的強度計算時，首先要知道齒輪上所受的力，這就需要對齒輪傳動作受力分析。當然，對齒輪傳動進行力分析也是計算安裝齒輪的軸及軸承時所必需的。

齒輪傳動一般均加以潤滑，嚙合輪齒間的摩擦力通常很小，計算輪齒受力時，可不予考慮。

沿嚙合線作用在齒面上的法向載荷Fn垂直于齒面，為了計算方便，將法向載荷Fn在節點P處分解為兩個相互垂直的分力，即圓周力Ft與徑向力Fr, 。由此得

Ft=2T1/d1 ； Fr=Fttanα ； Fn=Ft/cosα (a)

式中：T1—小齒輪傳遞的轉矩，N·mm；

d1—小齒輪的節圓直徑，對標準齒輪即為分度圓直徑，mm；

α—嚙合角，對標準齒輪，α=20°。

（二）齒根彎曲疲勞強度計算

輪齒在受載時，齒根所受的彎矩最大 ，因此齒根處的彎曲疲勞強度最弱。當輪齒在齒頂處嚙合時，處于雙對齒嚙合區，此時彎矩的力臂雖然最大，但力并不是最大，因此彎矩并不是最大。根據分析，齒根所受的最大彎矩發生在輪齒嚙合點位于單對齒嚙合區最高點。因此，齒根彎曲強度也應按載荷作用于單對齒嚙合區最高點來計算。由于這種算法比較復雜，通常只用于高精度的齒輪傳動（如6級精度以上的齒輪傳動）。

對于制造精度較低的齒輪傳動（如7，8，9級精度），由于制造誤差大，實際上多由在齒頂處嚙合的輪齒分擔較多的載荷，為便于計算，通常按全部載荷作用于齒頂來計算齒根的彎曲強度。當然，采用這樣的算法，齒輪的彎曲強度比較富余。

右邊動畫所示為齒輪輪齒嚙合時的受載情況。動畫演示為齒頂受載時，輪齒根部的應力圖。

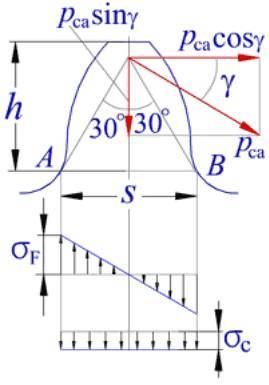
在齒根危險截面AB處的壓應力σc僅為彎曲應力σF的百分之幾，故可忽略，僅按水平分力pcacosγ所產生的彎矩進行彎曲強度計算。

假設輪齒為一懸臂梁，則單位齒寬（b＝1）時齒根危險截面的彎曲應力為

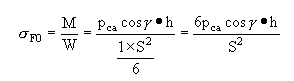
取，并將(a)式代入。對直齒圓柱齒輪，齒面上的接觸線長L即為齒寬b(mm)，得

令

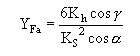
YFa是一個無量綱系數，只與齒輪的齒廓形狀有關，而與齒的大小（模數m）無關。因此，稱為齒形系數。S值大或h值小的齒輪，YFa的值要小些；YFa小的齒輪抗彎曲強度高。載荷作用于齒頂時的齒形系數YFa可查表查表查表查表確定。

齒根危險截面的彎曲應力為：

上式中的σF0僅為齒根危險截面處的理論彎曲應力，實際計算時，還應計入齒根危險截面處的過渡圓角所引起的應力集中作用以及彎曲應力以外的其它應力對齒根應力的影響，因而得齒根危險截面得彎曲強度條件式為

(b)

式中Ysa為載荷作用于齒頂時的應力校正系數（數值列于表<齒形系數及應力校正系數> ）。

令： φd=b/d1

φd成為齒寬系數，并將Fd=2T1/d1及m=d1/z1代入式(b),得

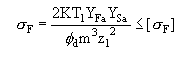
于是得

(c)

式(c)為設計計算式，式(b)為校核計算公式。

（三）齒面接觸疲勞強度計算

齒面接觸疲勞強度計算的基本公式為:

Fca為計算載荷,L為接觸線長度,為計算方便，取接觸單位長度上的計算載荷

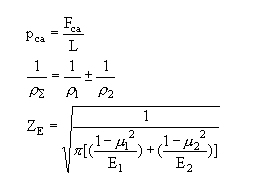
式中：ρ∑—嚙合齒面上嚙合點的綜合曲率半徑；

ZE—彈性影響系數，數值列于下表，則上式為

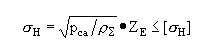
(d)

彈性影響系數ZE/()

注：表中所列夾布塑膠的泊松比μ為0.5，其余材料的μ均為0.3。

由《機械原理》得知，漸開線齒廓上各點的曲率（1/ρ）并不相同，沿工作齒廓各點所受的載荷也不一樣。因此按式(d)計算齒面的接觸強度時，就應同時考慮嚙合點所受的載荷及綜合曲率（1/ρ∑）的大小。對端面重合度

≤2的直齒輪傳動，如圖<齒面上的接觸應力>所示，以小齒輪單對齒嚙合的最低點（圖中C點）產生的接觸應力為最大，與小齒輪嚙合的大齒輪，對應的嚙合點是大齒輪單對齒嚙合的最高點，位于大齒輪的齒頂面上。

如前所述，同一齒面往往齒根面先發生點蝕，然后才擴展到齒頂面，亦即齒頂面比齒根面具有較高的接觸疲勞強度。因此，雖然此時接觸應力大，但對大齒輪不一定會構成威脅。由圖<齒面上的接觸應力>可看出，大齒輪在節處的接觸應力較大，同時，大齒輪單對齒嚙合的最低點（圖中D點）處接觸應力也較大。但按單對齒嚙合的最低點計算接觸應力比較麻煩，并且當小齒輪齒數z1≥20時，按單對齒嚙合的最低點所計算得的接觸應力與按節點嚙合計算得的接觸應力極為相近。為計算方便，通常即以節點嚙合為代表進行齒面的接觸強度計算。

下面即介紹按節點嚙合進行接觸強度計算的方法：

節點嚙合的綜合曲率為

輪齒在節點嚙合時，兩輪齒廓曲率半徑之比與兩輪的直徑或齒數成正比，即ρ2ρ1=d2/d1=z2/z1=u, 故得

小齒輪輪齒節點P處的 曲率半徑。對于標準齒輪，節圓就是分度圓，故得 ρ1=d1sinα/2

則:

取L＝b（b為齒輪設計工作寬度）,于是(d)式為:

令

——區域系數（標準直齒輪α=20°時，ZH＝2.5），則可寫為

MPa

將Ft=2T1/d1、φd=b/d1代入上式得 σH=

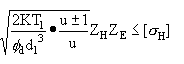
于是

mm

若將ZH＝2.5代入上面兩式,得

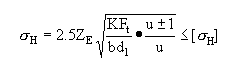
MPa

及

（四）齒輪傳動的強度計算說明

按齒根彎曲疲勞強度計算時，應將

/(YFa1YSa1) 或/(YFa2YSa2)中小者代入計算。 因配對齒輪的接觸應力相同，即σH1=σH2,故應將中小者代入公式進行計算。

當配對兩齒輪的齒面均屬硬齒面時，兩輪的材料，熱處理方法及硬度均可取成一樣的。設計這種齒輪傳動時，可分別按齒根彎曲疲勞強度及齒面接觸疲勞強度的設計公式進行計算，并取其中大者作為設計結果。

當用設計公式初步計算齒輪的分度圓直徑d1（或模數mn）時，動載系數Kv，齒間載荷分配系數Kα及齒向載荷分布系數Kβ不能預先確定，此時可選一載荷系數Kt(腳標t表示試選或試算值)(如取Kt=1.2～1.4)，則算出來的分度圓直徑（或模數）也是一個試算值的d1t（或mnt）,然后按d1t值計算齒輪的圓周速度，查取動載系數Kv，齒間載荷分配系數Kα，及齒向載荷分布系數Kβ，計算載荷系數K。若算得的K值與試選的Kt值相差不多，就不必修改原計算；若二者相差較大時，應按下式校正試算所得分度圓直徑d1t（或mnt）：

（來源：機械工業）

END