邊界對應定理
邊界對應定理基本信息
| 中文名 | 邊界對應定理 | 外文名 | theorem of boundary correspondence |
|---|---|---|---|
| 屬????性 | 復變函數幾何理論的基本定理之一 | 所屬學科 | 數學 |
| 所屬問題 | 復變函數論(幾何函數論) | 相關概念 | 共形映射,有界單連通區域等 |
定理2(邊界對應定理的逆定理,判斷解析函數單葉性的充分條件)
設單連通區域D及G,分別是兩條圍線
(i)
(ii)
則:(1)
證明設
其次,設
再設
綜合上述討論可知函數
【例1】如果將函數
由定理2(單葉性原理),
2100433B
邊界對應定理造價信息
黎曼定理指出某些區域可用單葉函數共形映射成圓盤,但無法說明已給區域與圓盤的邊界之間是否有對應關系。對于以約當曲線為邊界的區域,有一個比較簡單的結果。
定理1(邊界對應定理)設
(1) 有界單連通區域D與G的邊界分別為圍線
(2)
則
邊界對應定理常見問題
-
基礎邊界在哪啊,白色虛線框是笩板基礎邊界還是墊層邊界呢?——:白色虛線是筏板基礎外邊線的吧您看看您的基礎大樣圖
-
答:路面寬度不包路緣石含路平石,人行道寬度含路緣石和路側石。
-
你說的是理正的滲流分析模塊吧,我在幾個小型水庫上用過,據我的經驗一般只要“面邊界條件”輸入正確,那么“點邊界條件”可不用輸入,結果沒有影響。如果要非要輸入“點邊界條件”,則可以輸入下游水位與坡面交點,...
邊界對應定理文獻

 建筑退讓邊界計算
建筑退讓邊界計算
格式:pdf
大小:49KB
頁數: 4頁
評分: 4.5
2.3.1 定義 退線距離 :系指建筑物后退各種規劃控制線(包括:規劃道路、綠化隔離帶、鐵路隔離 帶、河湖隔離帶、高壓走廊隔離帶)的距離。 退界距離 :系指建筑物后退相鄰單位建設用地邊界線的距離。 城市道路 :系指在總體規劃和分區土地使用規劃中已確定的及詳細規劃中規定的主干 道、次干道、支路。 建筑工程與城市道路之間的距離 :系指建筑物臨城市道路一側最突出部分與道路紅線 之間的水平方向的垂直距離。 城市道路寬度 :系指該道路兩側規劃紅線之間的水平方向的垂直距離。 現有城市道路路面邊線 :當路面為單幅路時,系指路牙線;當路面為三幅路 (機動車道 與非機動車道之間以隔離帶分隔 )時,系指非機動車道路牙線。 2.3.2 退讓規劃道路紅線距離 一般規定: 1.不允許突入道路紅線的建筑突出物:建筑物的臺階、平臺、窗井、坡道、花池、散 水、地下室進排風口、地下建筑及建筑基礎;除基地內連接城市管線以
香農定理用來求信道的最大傳輸速率,即信道容量,當通過信道的信號速率超過香農定理的信道容量時,誤碼率顯著提高,信息質量嚴重下降。需要指出的是這里的信道容量只是理論上可以達到的極限,實際如何達到,該定理不能說明。
割線定理
定義
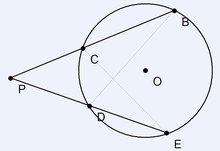
從圓外一點引圓的兩條割線,這一點到每條割線與圓交點的距離的積相等。
從圓外一點P引兩條割線與圓分別交于C,B,D,E,則有 PC·PB=PD·PE。如下圖所示。 (PA是切線)
英文名稱
Secant Theorem
概述
割線定理為圓冪定理之一(切割線定理推論),其他二為:
切割線定理
相交弦定理
證明
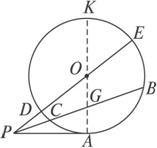
如圖直線PB和PE是自點P引的⊙O的兩條割線,則PC·PB=PD·PE.
證明:連接CE、DB
∵∠E和∠B都對弧CD
∴由圓周角定理,得 ∠E=∠B
又∵∠EPC=∠BPD
∴△PCE∽△PDB
∴PC:PD=PE:PB, 也就是PC·PB=PD·PE.
比較
割線定理與相交弦定理,切割線定理通稱為圓冪定理。
相交弦定理、切割線定理以及它們的推論統稱為圓冪定理。一般用于求線段長度。
- 相關百科
- 相關知識
- 相關專欄
- 邊界檢查
- 邊界網關協議
- 邊看邊學SIEMENS數控車床加工50例(1例1視頻)
- 邊緣融合器
- 邊角料
- 遼東學院裝備與材料學院
- 遼中縣土地局
- 遼寧一東電電力科技股份有限公司
- 遼寧三益家具制造有限公司
- 遼寧世紀金牛管業有限公司
- 遼寧東大東熱電器有限公司
- 遼寧東戴河新區友邦信息咨詢有限公司
- 遼寧東戴河新區當代置業有限公司
- 遼寧東方華升建設集團有限公司
- 遼寧東星節能新材有限公司
- 遼寧東正工程造價咨詢事務所有限公司
- 信貸擴張、房地產價格波動與銀行穩定理論及其經驗分析
- 合力矩定理在土建工程中的應用
- 實驗三戴維南定理驗證及有源單口網絡等效參數的測量
- 對新火電廠大氣污染物排放標準脫硫規定理解
- Hermite插值神經網絡權值和結構確定理論
- 施工企業共產黨員堅定理想信念措施
- 工業建筑可靠性鑒定理論與應用
- 受施工擾動影響土體環境穩定理論與變形控制
- 穩定理論的低碳鋼托架結構參數的優化設計
- 可變模糊集對立統一定理的水安全評價
- 數值分析課程中定理反講教學方式
- 壓力容器金屬材料進廠驗收最新規定理解
- 安全閥閥芯傳感器標定理論與驗證技術
- 不確定理論的電力系統脆弱性評估
- 壓差旁通閥壓差值再設定理論計算
- 巖體等效強度參數確定理論和方法