COST-231-Walfisch-lkegami 模型簡介
COST-231-Walfisch-Ikegami 模型基于Walfisch-Bertoni模型和Ikegami模型,廣泛地用于建筑物高度近似一致的郊區和城區環境,經常在移動通信系統(GSM/PCS/DECT/DCS)的設計中使用。在高基站天線情況下采用理論的Walfisch-Bertoni模型計算多屏繞射損耗,在低基站天線情況下采用測試數據計算損耗。
COST-231-Walfisch-lkegami 模型考慮了自由空間損耗、從建筑物頂到街面的損耗以及受街道方向影響的損耗,因此,可以計算基站發射天線高于、等于或低于周圍建筑物等不同情況的路徑損耗。COST 231-WI模型廣泛用于建筑物高度近似一致的郊區和城區環境。它是基于Walfisch-Bertoni模型和Ikegami模型得到的。在使用低基站天線時該模型采用理論的Walfisch-Bertoni模型計算多屏繞射損耗;在使用低基站天線時采用測試數據。該模型也考慮了自由空間損耗、從建筑物頂到街面的損耗以及街道方向的影響。
COST-231-Walfisch-lkegami 模型造價信息
COST-231-Walfisch-lkegami 模型簡介常見問題
-
你要找那一年的S231圖集的呀
-
它是將復雜的系統分解為若干子系統要素,利用人們的實踐經驗和知識以及計算機的幫助,最終構成一個多級遞階的結構模型。此模型以定性分析為主,屬于結構模型,可以把模糊不清的思想、看法轉化為直觀的具有良好結構關...
-
2018已經下架了沒有程序可以共享了可以找官方客服或者是分支索取
COST-231-Walfisch-lkegami 模型簡介文獻

 于老師講座-12345模型--8.5
于老師講座-12345模型--8.5
格式:pdf
大小:662KB
頁數: 12頁
評分: 4.4
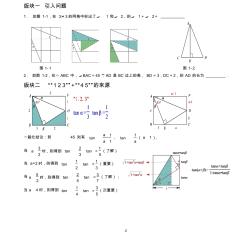
2 版塊一 引入問題 1. 如圖 1-1,在 3×3的網格中標出了∠ 1 和∠ 2,則∠ 1+∠ 2= 圖 1- 1 圖 1- 2 2. 如圖 1-2,在△ ABC 中,∠BAC=45°,AD 是 BC 邊上的高, BD=3,DC=2,則 AD 的長為 _________. 版塊二 “1 2 3”+“4 5”的來源 一般化結論:若 45 則有 1tan 1 a a , 1tan a ( 1a ), 當 3 2 a 時,則得到 2 1 tan tan = 3 5 (了解) 當 a=2時,則得到 1 1tan tan = 2 3 (重要) 當 5 2 a 時,則得到 2 3tan tan = 5 7 (了解) ; 當 4a 時,則得到 1 3tan tan = 4 5 (次重要) 3 【例 1】(濟南市中考題)如圖 2-1, AOB 是放置在正方形網絡中的一個角,則 cos AOB 的值是 .
模型實驗一般步驟
(1)先根據實驗場地、模型制作和測量條件定出長度比尺;
(2)以選定的比尺縮小或放大原型的幾何尺寸,得出模型的幾何邊界;
(3)根據對流動受力情況的分析,滿足對流動起主要作用的力相似,選擇模型律;
(4)按選用的模型律,確定流速比尺及模型的流量。
模型實驗模型實驗數據
模型實驗數據可以分為兩大類:一類是無量綱的量,由于模型與原型流動相似,模型值與原型值對應相等,不必進行換算;一類是有量綱的量,如流動阻力、壓強、流速分布等,則需要按照所選擇的相似準則得出的比尺關系進行換算。素進行獨立控制。與現場實測相比,可進行方案的前期優化,具有省時、省力的優點。
模型實驗各種研究方法的比較
(1)理論分析法——有時不同的理論方法得到的解析解不同,有時又難以求解。
(2)數值計算一仿真分析——由于很多工程中的一些不確定因素,輸入參數難以精確,還有模型簡化等問題,存在一定局限性。
(3)現場實測——只有在工程施工過程中進行,投入較大,周期長。
(4)模型實驗——可使工程中發生的現象在實驗室中再現出來,而且還可以對實驗中主要原因。
物理模型
也稱實體模型,又可分為實物模型和類比模型。①實物模型:根據相似性理論制造的按原系統比例縮小(也可以是放大或與原系統尺寸一樣)的實物,例如風洞實驗中的飛機模型,水力系統實驗模型,建筑模型,船舶模型等。②類比模型:在不同的物理學領域(力學的、電學的、熱學的、流體力學的等)的系統中各自的變量有時服從相同的規律,根據這個共同規律可以制出物理意義完全不同的比擬和類推的模型。例如在一定條件下由節流閥和氣容構成的氣動系統的壓力響應與一個由電阻和電容所構成的電路的輸出電壓特性具有相似的規律,因此可以用比較容易進行實驗的電路來模擬氣動系統。
數學模型
用數學語言描述的一類模型。數學模型可以是一個或一組代數方程、微分方程、差分方程、積分方程或統計學方程,也可以是它們的某種適當的組合,通過這些方程定量地或定性地描述系統各變量之間的相互關系或因果關系。除了用方程描述的數學模型外,還有用其他數學工具,如代數、幾何、拓撲、數理邏輯等描述的模型。需要指出的是,數學模型描述的是系統的行為和特征而不是系統的實際結構。
結構模型
主要反映系統的結構特點和因果關系的模型。結構模型中的一類重要模型是圖模型。此外生物系統分析中常用的房室模型(見房室模型辨識)等也屬于結構模型。結構模型是研究復雜系統的有效手段。
仿真模型
通過數字計算機、模擬計算機或混合計算機上運行的程序表達的模型。采用適當的仿真語言或程序, 航海模型(6張)物理模型、數學模型和結構模型一般能轉變為仿真模型。關于不同控制策略或設計變量對系統的影響,或是系統受到某些擾動后可能產生的影響,最好是在系統本身上進行實驗,但這并非永遠可行。原因是多方面的,例如:實驗費用可能是昂貴的;系統可能是不穩定的,實驗可能破壞系統的平衡,造成危險;系統的時間常數很大,實驗需要很長時間;待設計的系統尚不存在等。在這樣的情況下,建立系統的仿真模型是有效的。
例如,生物的甲烷化過程是一個絕氧發酵過程,由于細菌的作用分解而產生甲烷。根據生物化學的知識可以建立過程的仿真模型,通過計算機尋求過程的最優穩態值并且可以研究各種起動方法。這些研究幾乎不可能在系統自身上完成,因為從技術上很難保持過程處于穩態,而且生物甲烷化反應的起動過程很慢,需要幾周的時間。但如果利用(仿真)模型在計算機上仿真,則甲烷化反應的起動過程只需要幾分鐘的時間。
工業模型
工業模型,俗稱手板.首板模型,和快速成型,主要制作方法有CNC加工,激光快速成型和硅膠模小批量生產,廣泛應用于工業新產品設計研發階段,在最短的時間內加工出和設計一致的實物模型,設計師進行產品外觀確認和功能測試等,從而完善設計方案.達到降低開發成本.縮短開發周期,迅速獲得客戶認可的目的。
阻尼模型由于阻尼材料內部結構的復雜性,材料的阻尼特性也是很復雜的,要想建立一個精確的數學模型來表示其性能也比較困難。對于阻尼材料來說,應力、應變、時間、溫度等變量之間的函數關系通常是非線性的,表示材料特性的狀態方程又受到諸如外力、溫度場、磁場、化學反應和輻射等外部環境的干擾。因此,描述材料的阻尼特性通常都采用近似的表示方法。
人們在長期的研究過程中已經建立了幾種阻尼模型,包括標準線性模型、通用化標準模型、復模量模型、分數導數模型、GHM模型等。這些模型具有各自不同的特點和適用范圍,下面分別加以介紹。
阻尼模型標準線性
對于一些小阻尼的材料,或者對于在一定的限制范圍內(如小振幅情況下)聚合材料等大阻尼材料,可以用標準線性模型來描述。其狀態方程是一種線性模型表示法:
σ α′dσdt=Eε δ′Edεdt(1)
式中E為彈性模量,α′為應力衰減常數,δ′為應變衰減常數。可以看出,該式形式簡單,所以使得計算簡單。但是與其它方法相比,它的使用范圍受到很大的限制,只能在前面所說的小范圍內使用。根據應用情況,這種模型主要用在地表環境中。比如范家參用該模型對固體在半平面內傳播的地震波進行了計算,得到了地震波的解析解。杜啟振等人在弱黏滯性條件下采用該模型對粘彈性波在地球介質中的傳播用有限元方法進行了計算,得到了波場傳播特征。孫昱等人將樁周圍的土對樁的作用以標準線性固體模型來表示,研究了樁周土對樁的動力作用 。
阻尼模型通用化標準
為了減少上述模型在使用時的限制,可以在(1)式中引入σ和ε的導數項,使它更符合實際情況,這時得到:
σ ∑∞n=1α′ndnσdtn=Eε E∑∞n=1δ′ndnεdtn(2)
式中E為彈性模量,α′n為應力衰減常數,δ′n為應變衰減常數。n為導數項的階數,其值可以根據實際情況適當的選擇。這種模型是標準模型的推廣,主要用于理論分析上,在實際中由于其實際計算的復雜性而應用較少。由于粘彈性材料(VEM)的剪切模量隨溫度和頻率的變化而變化,以上的模型的應用無法描述這一特性,所以一般只適用于弱粘彈性材料。而以下的幾種模型主要用于對各種VEM進行計算。其中用得較多的就是復模量模型。
阻尼模型復模量
復模量模型又分為復常數模量和頻變復模量模型,是分析粘彈性材料結構動力學響應特性較為有效的方法 。
復常數模量模型在許多的研究中均用復常數模量形式,即:
E=ER jEI=ER(1 jη)(3)
式中ER是存貯模量,表示存貯能量的能力;EI是損耗模量,表示能量的耗散程度;j=-1,是虛數單位;η是材料的損耗因子,有:
η=EIER(4)
在文獻中還有這樣一種復模量的定義:
E*=σε=σ0ε0(cosα isinα)(5)
對比(3)式和(5)式可得:
彈性模量E=σ0ε0cosα(6)
損耗因子η=tgα(7)
則粘彈性材料的應力-應變關系為:
σ=E*ε=E(1 iη)ε(8)
上述模型中,各量均為常數,并沒有考慮頻變特性,因此其適用范圍只限于頻變較小的情況。比如黃潤秋等人在對隧址區山體的地震動作用特點進行研究的過程中,采用復模量模型很好的模擬了巖石體的動力學性能。Rikards等構建了復合夾層梁、板的超級單元,夾層粘彈性材料特性采用了復模量模型進行描述,但是沒有考慮粘彈性材料特性隨頻率而變化的事實。秦惠增等人借助有關粘彈性材料結構動力學分析的復模量模型,推出簡諧激勵作用下形狀記憶合金(SMA)層面內的變形和應力之間的關系。
頻變復模量模型
復常數模量模型雖然可以使得計算簡單,但是不能反映出材料的頻變性質。人們為了反映材料的頻變性質,通過實驗方法由數據擬合來得到頻變的復模量:
E(ω)=ER(ω)(1 jηv(ω))(9)
則粘彈性材料的應力-應變關系為:
σ=E(ω)ε=ER(ω)(1 jηv(ω))ε(10)
其中:ER(ω)=aEωbE,ηv(ω)=aηωbη
aE、aη及bE、bη均為擬合常數。頻變復模量模型可以反映VEM的頻變特性,與常數復模量模型相比,其適用范圍更加廣泛,結果也更準確。比如粱軍用該模型對復合材料的動態粘彈性能進行了研究,分析了材料復模量隨夾雜體積分數、載荷頻率之間的變化規律。任志剛等人采用頻變復模量模型模擬了夾層粘彈性材料特性的頻率相關性,并提出了采用模態應變能迭代及復特征值迭代求解復合夾層結構的各階頻率及損耗因子的方法。但與復常數模量模型一樣,它無法揭示VEM的力學本質,計算也較為復雜。2100433B
- 相關百科
- 相關知識
- 相關專欄
- CPM-M4
- CQB-F型氟塑料磁力驅動泵
- CR12模具鋼開裂
- CSA認證
- CSF-600
- CSJ500中藥粗碎機
- CSJB系列橡塑類粗碎機
- CT film
- CVC軋機
- CWG
- Casaitaliana(卡薩伊塔蓮娜)
- CimatronE10.0 模具設計看圖速成
- CimatronE8模具設計實例圖解
- Coway AP-2510EH
- Coway BAS16-A
- Cr6WV
- 永磁同步電機簡介
- 新型基于熱力學法的水泵效率數學模型及應用
- 基于閉環反饋優化的IDC基礎設施造價評估模型
- 云計算模型在船體復雜結構件裝配和三維建模中的應用
- 基于GIS的礦產資源的潛力評價的自動制圖模型
- 有孔管樁靜壓沉樁超孔隙水壓力消散室內模型試驗分析
- 柘溪水電站引水隧洞鋼筋混凝土襯砌仿真模型試驗
- 應用Block模型高大空間分層空調的溫度分布
- 圓形隧道施工對不同深度地層沉降影響的模型試驗
- 以色列ELI自清洗網式過濾器和淺層介質過濾器簡介
- 基于粗糙集和灰聚類理論的IT項目評標決策模型
- 云南電網電力系統動態模型仿真實驗室建設可行性
- 四層結構模型的變電站綜合自動化系統設計與實現
- 有關水利水電勘測設計技術標準體系情況的簡介
- 關于排煙積灰水平管道來流繞過管道附著概率模型
- 關于進一步加強上海市建筑信息模型技術應用推廣通知
