靜定反力靜定結構的受力分析
幾種靜定結構的受力分析大致相同,繪制內力圖的一般步驟如下:
①求反力(懸臂梁可以不必求反力)。
②定點:選外力的不連續點作為控制截面,如集中力及集中力偶作用點兩側的截面;分布荷載的起迄點。用截面法求出這些截面的內力值,并將它們在內力圖的基線上用縱距繪出。這樣就定出了內力圖上的各控制點。
③聯線:根據結構在各控制點之間內力圖形狀特點,分別用直線或曲線相聯,即得內力圖。若相鄰控制截面之間無荷載,則該段彎矩圖為斜直線。當繪制彎矩圖時,若相鄰控制截面之間有荷載作用,則該段可按疊加法繪出其彎矩圖。
靜定反力造價信息
靜定反力靜定結構
對于幾何不變的且無多余約束的結構來說,由于其可列出的靜力平衡方程式數目與未知約束力數目相等,故其全部反力和內力僅用靜力平衡方程就可求得,且解是唯一的,這種結構就是靜定結構。
根據靜定結構在一定的外荷載作用下,其反力與內力的解答是唯一的,可得其在靜力方面的另兩個特性:
①由于靜力平衡方程與結構的材質和截面尺寸無關,故靜定結構的反力、內力與結構的材質、截面尺寸無關;
②在靜定結構中,除荷載外,其他外因如溫度變化、支座移動、制造誤差、材料收縮等都不能使結構產生反力和內力。這是因為當靜定結構上荷載為零時,由靜力平衡條件可知,其反力、內力必都為零。
幾種典型的靜定結構有:梁、剛架、桁架等。
靜定反力靜力學
力學的一個部分,它研究物體在力的作用下處于平衡的規律,建立各種力系的平衡條件。靜力學還研究力系的簡化和物體受力的基本分析方法。物體受到幾個力的作用,仍保持靜止狀態,或勻速直線運動狀態,或繞軸勻速轉動狀態,叫做物體處于平衡狀態,簡稱物體的平衡。處于平衡狀態的物體,可以是靜平衡,即物體既無平動,又無轉動,保持靜止,也可以是動平衡,即物體作勻速直線運動,或勻角速轉動。無論是處于靜平衡,還是動平衡,物體的受力情況是沒有區別的。區別在于物體的初始狀態,即物體開始處于力平衡的瞬時,它為靜止的,還是平動或轉動的。
靜力學發展時期,是從公元前3世紀,到16世紀伽利略奠定動力學基礎為止。阿基米德是使靜力學成為一門真正科學的奠基者。著名的意大利藝術家、物理學家和工程師達·芬奇,對靜力學的建立作出了重要貢獻。靜力學的基本物理量是力、力偶和力矩。學科內容主要包括以下幾個方面:
①力作用于物體的效應分為外效應和內效應。外效應是指力使整個物體對外界參照系的運動變化;內效應是指力使物體內各部分相互之間的變化。對剛體不必考慮內效應。
②靜力學公理。靜力學的全部推理是以幾個簡單公理為基礎的。這些公理是人類在長期的生產實踐中積累起來的力的知識的總結。它反映了作用在剛體上的力的最簡單、最基本的屬性,這些公理的正確性是可以通過實驗來驗證的,但不能用更基本的原理來證明。
公理Ⅰ: 二力平衡原理。
公理Ⅱ: 加減平衡力系原理。可在作用于剛體上的已知力系中增加一個平衡系,或者從這個力系中減去一個平衡系,而不改變原力系對剛體的作用效果。
公理Ⅲ: 力的平行四邊形法則。
公理Ⅳ: 作用和反作用定律。
公理Ⅴ: 硬化原理。設一個變形體在一個力系作用下,處于平衡狀態,若將這種狀態下的變形體看成剛體,則其平衡狀態不被破壞。
靜力學知識在工程技術中有直接的應用。例如,對軸上零件的受力分析,從而合理地布置軸承;應用平衡條件求出軸承反力,作為選用軸承的一個依據;對考慮摩擦力的平衡問題進行分析,得出某些零件的自鎖條件,以便正確地設計這些零件等等。
靜定反力約束反力
約束的作用力。指被約束體受約束體的作用力,簡稱約束力。約束反力分動靜兩類,動約束力亦稱附加動反力,和被約束體的加速運動有關。例如,電梯以加速度a上升,其中質量為m的人受向上的動約束反力大小為ma;繞軸轉動的偏心轉子要受到軸承的動約束反力,軸承必受到動壓力。靜約束力大小取決于被約束物體所受的主動力,方向與被阻礙的運動方向相反,作用點為約束和被約束體的接觸點。例如,對于光滑接觸面,約束力通過接觸點垂直公切面指向被約束體;對于光滑球鉸鏈,約束力通過鉸心,方向不定,但可用三個未定的垂直分量表示。在工程技術方面,約束力的分析計算十分重要。而對于高速轉動的轉子,動約束力有時能達到靜約束力的10倍以上,這種力的消除成為高速轉動機械的重要技術問題。理論上講,使轉軸通過轉子的質量中心并成為慣性主軸就可使這種動約束反力為零。
幾種典型的靜定結構有靜定梁、靜定剛架、靜定三鉸拱、靜定桁架和靜定組合結構等。公交站臺的雨棚是用剛性結點連接的三根直桿所組成的T字結構,柱子固定于基礎中,屬于典型的靜定剛架結構。北京頤和園昆明湖上的十七孔橋就是由十七個靜定三鉸拱所構成,單個橋跨的破壞不會引起整個橋體的連續倒塌。靜定三鉸拱和靜定桁架結構在制造誤差和溫度改變作用下均不會產生內力,也常用作對溫度敏感的大跨度房屋屋蓋結構,如大型商場、禮堂和展覽館等。陜西秦始皇兵馬俑展覽館屋蓋體系很好的利用了三鉸剛拱架的靜定特性,既實用又美觀。
在均布荷載作用下,兩跨連續梁相對于兩跨靜定梁,連續梁結構剛度大、變形小,跨中彎矩的最大值可以大幅降低,但其支座有負彎矩產生。當結構存在溫度變化和支座沉降情況時,兩跨連續梁和兩跨靜定梁均會產生一定程度的變形,兩跨連續梁在中間支座處會出現較大正彎矩,而兩跨靜定梁則無彎矩產生。
超靜定結構雖然具有較好的抵抗破壞能力,在多余約束被破壞的情況下仍能保持其幾何不變性,但在工 程應用時易受到溫度變化、制造誤差以及支座沉降等因素的影響。靜定結構應對突然破壞的防護能力較弱, 但其受力特點不受材料影響,其受力狀態不易被外界干擾。在對溫度變化、制造誤差以及支座沉降敏感的結構中,采用靜定結構比超靜定結構更為合適。由此得出,任何事物都具有兩面性,在某種特定情況下,靜定結構反而會比超靜定結構更加適用工程實際。 2100433B
靜定反力靜定結構的受力分析常見問題
-
簡單的定義就是,靜定結構的自由度數量和約束數量相等,超靜定結構是約束數量大于自由度數量。也就是說,靜定結構只要有一個約束出現故障失效,那么整個結構就成為可變結構了。而超靜定有多余的約束,個別約束失效了...
-
從幾何構造分析的角度看,結構必須是幾何不變體系。根據多余約束 n ,幾何不變體系又分為: 有多余約束( n > 0)的幾何不變體系——超靜定結構; 無多余約束( n = 0)的幾何不變體系——靜...
-
靜定結構和超靜定結構的區別:靜定結構是指僅用平衡方程可以確定全部內力和約束力的幾何不變結構。超靜定結構是指具有多余約束的幾何不變體系,又稱靜不定結構。拓展資料靜定結構──無多余約束的幾何不變結構,是實...
靜定反力靜定結構的受力分析文獻

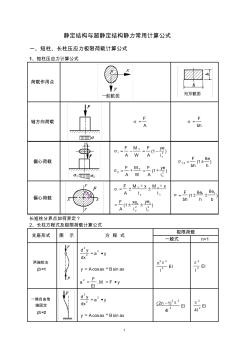 靜定結構與超靜定結構靜力計算公式
靜定結構與超靜定結構靜力計算公式
格式:pdf
大小:338KB
頁數: 8頁
評分: 4.7
1 靜定結構與超靜定結構靜力常用計算公式 一、短柱、長柱壓應力極限荷載計算公式 1、短柱壓應力計算公式 荷載作用點 軸方向荷載 A F bh F 偏心荷載 )1( 21 x Y i ye A F W M A F )1( 22 x Y i ye A F W M A F ) 6 1(2,1 h e bh F 偏心荷載 )1( 22 x y y x x x y Y i ye i xe A F I xM I xM A F ) 66 1( b e h e bh F yx 長短柱分界點如何界定? 2、長柱方程式及極限荷載計算公式 支座形式 圖 示 方 程 式 極限荷載 一般式 n=1 兩端鉸支 β=1 ya dx yd 2 2 2 axBaxAy sincos yFM EI F a ,2 EI l n 2 22 EI l 2 2 一端自由他 端固定 β=2 ya dx yd 2 2 2 axB
幾何不變體系
靜定梁是沒有多余約束的幾何不變體系,其反力和內力只用靜力平衡方程就能確定, 這是靜定梁的基本靜力特征。梁以受彎形變為主,主要內力為軸力、剪力和彎矩,靜定梁是一種最常見的靜定結構(無多余約束的幾何不變體系)。對應靜定結構還有一種有多余約束( n > 0)的幾何不變體系——超靜定結構。2100433B
首先判斷其外超靜定次數,再判斷內超靜定次數,二者之和為系統的總超靜定次數。
反力在結構計算上,可提供平衡條件,用以推算結構內力,并進一步分析結構變形量。 某些結構分析方法,會以假設反力的方式,減少靜不定的支承形式,此種假設反力,稱作靜不定余力或贅力(Redundant)。
分類:柔體約束,光滑接觸面約束,可動鉸支座,固定鉸支座,固定端支座。
可以根據該反力墻試驗系統的設計指標和受力特點,提出了合理的結構布置方案 。通過有限元分析軟件ABAQUS和MIDAS Gen建立了反力墻試驗系統的整體模型,進行了最不利試驗工況下的承載力分析、變形分析和應力分析。
還可以利用FLAC3D建立鋼管頂進過程的數值模型 ,對鋼管頂進過程中提供反力的結構進行分析。
- 相關百科
- 相關知識
- 相關專欄
- 靜定結構
- 靜強度分析
- 靜強度實驗系統
- 靜態[壓力]試驗
- 靜態吸附
- 靜態差分GPS測量儀
- 靜態數據采集系統
- 靜態澆注空心管坯
- 靜態試驗
- 靜態試驗機
- 靜態負荷特性
- 靜態驗收
- 靜揚程
- 靜摩擦系數
- 靜止變流器
- 靜止同步調相機
- 基于壓電堆驅動器的噴嘴擋板式氣體控制閥
- 磷銨技術改造五大磷肥工程的建議
- 以大豆油多元醇制備的硬質聚氨酯泡沫塑料的性能
- 逆變TIG焊機接觸引弧電路的設計(引弧電路)
- 應用模糊數學理論對公路工程建設項目方案的綜合評價
- 可替代現有隔熱保溫材料的新型材料
- 以貫穿項目為核心載體的建筑工程技術專業素材庫建設
- 多逆變器太陽能光伏并網發電系統的組群控制方法
- 影響萘高效減水劑與普通硅酸鹽水泥適應性的關鍵因素
- 在全縣非煤礦山和危化企業安全生產工作會議上的講話
- 中國工程造價咨詢業的發展趨勢
- 支持并行工程和智能CAPP的制造資源建模技術
- 中共重慶市委重慶市人民政府關于建設平安重慶的決定
- 智能建筑工程報警與電視監控系統前端設備的安裝施工
- 在“建筑節能與居住舒適”專題技術交流會議上的講話
- 以MSP430FW427為核心的遠程數字水表設計
